An LCG (Linear congruential generator) is a simplest PRNG (Pseudorandom number generator) and can be cracked easily.
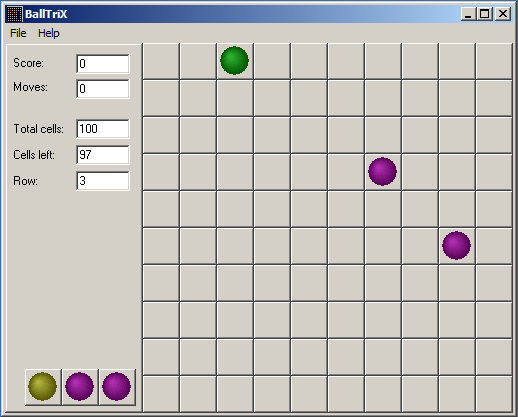
Here is a clone of a very popular "color lines" game (https://archive.org/download/BallTriX_1020).
In its internals we can find that it uses standard MSVC rand() function, like that:
uint32_t MSVC_rand()
{
g_seed = 214013 * g_seed + 2531011;
return (g_seed & 0x7FFF0000) >> 16;
};
The game places 3 balls at each step. Each ball has the following characteristics: row, column and color. It's easy to see in debugger, that rand() function is called 3 times for each step. Row and column are computed like that:
rand() % 10
... while color:
rand() % 5
At each step, rand() is called twice to get row and column, and then 3rd time to get color.
PRNG facility is initialized like that: srand(time(NULL)).
Let's see, if we can find a way to predict next balls' placement.
For this task, we are going to recover PRNG state. And I've found that 6 steps are enough to recover it. This problem can be solved using SMT-solver, but this is overkill; state is 32-bit variable, so it can be found using simple brute-force.
First, we run it, and in debugger, we can see that 6 triplets is generated using rand():

3 balls are placed and the game is also prepared other 3 balls. Now we see that at this step, the game is already know where the next 3 balls will be placed.
Now I'm moving topmost ball one step aside:
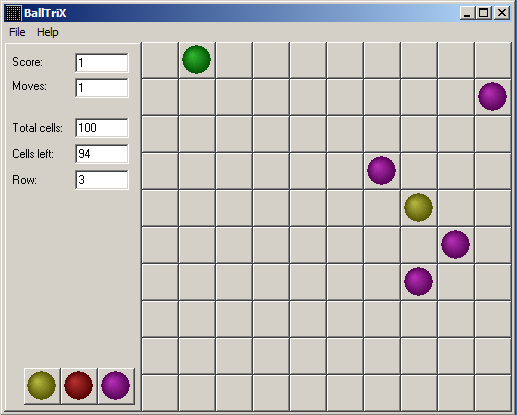
Now we got 6 pair of coordinates, and we can brute-force PRNG state. I didn't map colors to its numbers, so we ignore them completely.
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#define GROUP1_TRIPLET1_COL 2
#define GROUP1_TRIPLET1_ROW 0
#define GROUP1_TRIPLET2_COL 6
#define GROUP1_TRIPLET2_ROW 3
#define GROUP1_TRIPLET3_COL 8
#define GROUP1_TRIPLET3_ROW 5
#define GROUP2_TRIPLET1_COL 9
#define GROUP2_TRIPLET1_ROW 1
#define GROUP2_TRIPLET2_COL 7
#define GROUP2_TRIPLET2_ROW 6
#define GROUP2_TRIPLET3_COL 7
#define GROUP2_TRIPLET3_ROW 4
uint32_t g_seed;
uint32_t MSVC_rand()
{
g_seed = 214013 * g_seed + 2531011;
return (g_seed & 0x7FFF0000) >> 16;
};
void chk_seed(uint32_t seed)
{
int col[6];
int row[6];
int color[6];
g_seed=seed;
// generate 6 triplets:
for (int i=0; i<6; i++)
{
col[i]=MSVC_rand() % 10;
row[i]=MSVC_rand() % 10;
color[i]=MSVC_rand() % 5;
};
int group1=0, group2=0;
// we know coordinates, but we don't know order in which they appeared
// so we suppose that each triple could be generated at any point...
for (int i=0; i<3; i++)
{
if (col[i]==GROUP1_TRIPLET1_COL && row[i]==GROUP1_TRIPLET1_ROW)
group1|=1;
if (col[i]==GROUP1_TRIPLET2_COL && row[i]==GROUP1_TRIPLET2_ROW)
group1|=2;
if (col[i]==GROUP1_TRIPLET3_COL && row[i]==GROUP1_TRIPLET3_ROW)
group1|=4;
if (col[3+i]==GROUP2_TRIPLET1_COL && row[3+i]==GROUP2_TRIPLET1_ROW)
group2|=1;
if (col[3+i]==GROUP2_TRIPLET2_COL && row[3+i]==GROUP2_TRIPLET2_ROW)
group2|=2;
if (col[3+i]==GROUP2_TRIPLET3_COL && row[3+i]==GROUP2_TRIPLET3_ROW)
group2|=4;
};
if (group1==7 && group2==7)
{
printf ("seed 0x%x is OK\n", seed);
printf ("next points are probably these:\n");
for (int group=0; group<4; group++)
{
int new_col[3];
int new_row[3];
int new_color[3];
for (int i=0; i<3; i++)
{
new_col[i]=MSVC_rand() % 10;
new_row[i]=MSVC_rand() % 10;
new_color[i]=MSVC_rand() % 5;
printf ("col=%d row=%d color=%d\n", new_col[i], new_row[i], new_color[i]);
};
for (int r=0; r<10; r++)
{
for (int c=0; c<10; c++)
{
int put_it=0;
for (int i=0; i<3; i++)
if (new_col[i]==c && new_row[i]==r)
put_it=1;
printf (put_it ? "*" : ".");
};
printf ("\n");
};
printf ("\n");
};
};
};
int main()
{
// MSB of state isn't used at all, so we don't touch it
for (uint32_t seed=0; seed<0x80000000; seed++)
chk_seed(seed);
};
It took ~80 seconds on my somewhat outdated Xeon E3-1220. This is enough to get one single candidate:
seed 0x5b5341db is OK next points are probably these: col=3 row=3 color=0 col=6 row=2 color=2 col=8 row=9 color=4 .......... .......... ......*... ...*...... .......... .......... .......... .......... .......... ........*. col=4 row=7 color=4 col=1 row=0 color=4 col=0 row=3 color=0 .*........ .......... .......... *......... .......... .......... .......... ....*..... .......... .......... col=2 row=9 color=3 col=3 row=9 color=0 col=7 row=0 color=2 .......*.. .......... .......... .......... .......... .......... .......... .......... .......... ..**...... col=2 row=3 color=4 col=2 row=5 color=1 col=9 row=6 color=4 .......... .......... .......... ..*....... .......... ..*....... .........* .......... .......... ..........
Is it correct? Let's move topmost ball again couple of times:
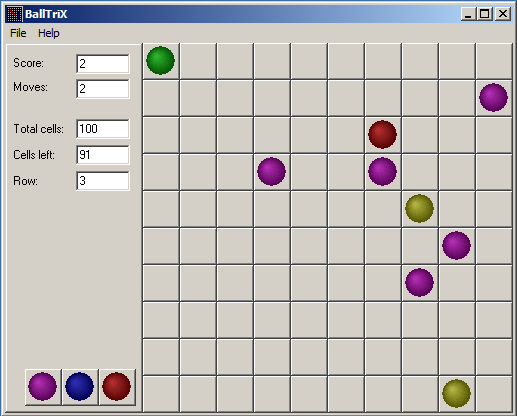
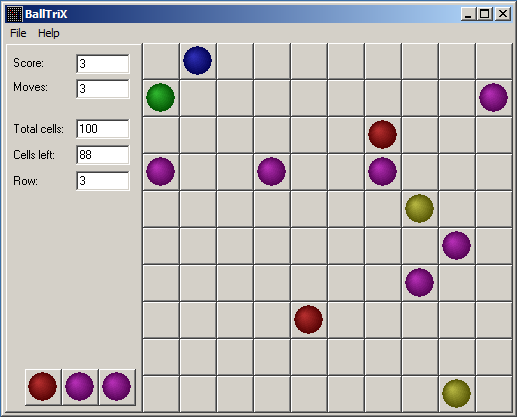
It seems so.
This is the way we can predict all further balls placements without touching debugger.
Since PRNG is initialized using current UNIX time, this can narrow brute-force process, if the current time (or day) is known.
What happens if the ball is to be placed to the occupied cell? Will rand() be called again?
LCG shouldn't be used at all, maybe except of embedded environments where code size is critical. Mersenne twister is much better, it has bigger internal state.
Even more, you can use block cipher as PRNG, or your favorite hash function: just hash your initial seed at the first step, then hash results of hashing in infinite loop, this can produce enough entropy to have the same features as PRNG, but it will not be crackable as easily as LCG.
More ideas and insights: RFC4086: "Randomness Requirements for Security".
The first part of "The Art of Intrusion: The Real Stories Behind the Exploits of Hackers, Intruders and Deceivers" book by Kevin Mitnick has a story about cracking a slot machine in casino that relied on a simple 32-bit LCG.
UPD: at reddit.
