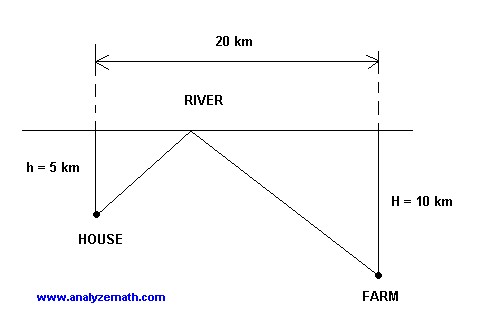
The problem I found here:
The diagram below shows the path that Wilson follows every morning to take water from the river to his farm. Help Wilson minimize the total distance traveled from his house to the farm. Where should he get water from the river?

Yes, this can be solved easily by hand using calculus, but the problem is that my knowledge of it is rudimentary. However, I can use my MK85 toy SMT-solver...
(declare-fun x () (_ BitVec 32)) (declare-fun house_to_river () (_ BitVec 32)) (declare-fun farm_to_river () (_ BitVec 32)) (declare-fun river_length () (_ BitVec 32)) (declare-fun river_length_minus_x () (_ BitVec 32)) (declare-fun hypot1 () (_ BitVec 32)) (declare-fun hypot2 () (_ BitVec 32)) (assert (= house_to_river (_ bv5000 32))) (assert (= farm_to_river (_ bv10000 32))) (assert (= river_length (_ bv20000 32))) (assert (= river_length_minus_x (bvsub river_length x))) (assert (= (bvand #xfffffff0 (bvmul_no_overflow hypot1 hypot1)) (bvand #xfffffff0 (bvadd (bvmul_no_overflow x x) (bvmul_no_overflow house_to_river house_to_river))))) (assert (= (bvand #xfffffff0 (bvmul_no_overflow hypot2 hypot2)) (bvand #xfffffff0 (bvadd (bvmul_no_overflow river_length_minus_x river_length_minus_x) (bvmul_no_overflow farm_to_river farm_to_river))))) (minimize (bvadd hypot1 hypot2)) (check-sat) (get-model)
Since it operates only on integers, there can be a problem of finding square root. But I'm using a dirty hack here: I compare only high 28 bit ignoring low 4 bits.
; on Intel(R) Core(TM)2 Duo CPU T9600 @ 2.80GHz clocked at 2.1 GHz ; ./MK85 1.smt > 1.result 153.27s user 0.26s system 98% cpu 2:35.96 total sat (model (define-fun farm_to_river () (_ BitVec 32) (_ bv10000 32)) ; 0x2710 (define-fun house_to_river () (_ BitVec 32) (_ bv5000 32)) ; 0x1388 (define-fun hypot1 () (_ BitVec 32) (_ bv8336 32)) ; 0x2090 (define-fun hypot2 () (_ BitVec 32) (_ bv16664 32)) ; 0x4118 (define-fun river_length () (_ BitVec 32) (_ bv20000 32)) ; 0x4e20 (define-fun river_length_minus_x () (_ BitVec 32) (_ bv13330 32)) ; 0x3412 (define-fun x () (_ BitVec 32) (_ bv6670 32)) ; 0x1a0e )
This may be impractical, but as a proof-of-concept...
We can also solve it using simulated annealing:
#!/usr/bin/env python3
import math, itertools
import random
from simanneal import Annealer
import re, sys
# requires https://github.com/perrygeo/simanneal
RIVER_LENGTH=20000
HOUSE_TO_RIVER=5000
FARM_TO_RIVER=10000
MAX_X=RIVER_LENGTH
class TestProblem(Annealer):
def __init__(self, state):
super(TestProblem, self).__init__(state)
def move(self):
if random.randint(0, 1)==0:
self.state[0]=self.state[0]+5
else:
self.state[0]=self.state[0]-5
def energy(self):
x=self.state[0]
path = math.sqrt(x**2 + HOUSE_TO_RIVER**2) + math.sqrt((RIVER_LENGTH-x)**2 + FARM_TO_RIVER**2)
return path
if __name__ == '__main__':
init_state = [0.0]
test = TestProblem(init_state)
test.steps = 200000
# since our state is just a list, slice is the fastest way to copy
test.copy_strategy = "slice"
state, e = test.anneal()
print()
print ("x =", state[0])
Temperature Energy Accept Improve Elapsed Remaining
2.50000 25000.41 99.60% 49.35% 0:00:03 0:00:00
x = 6665.0
Let's recheck using Wolfram Mathematica:
In[]:= Minimize[Sqrt[x^2 + 5^2] + Sqrt[(20 - x)^2 + 10^2], x] // N
Out[]:= {25., {x -> 6.66667}}
I.e., first third of the river is the correct answer.

Yes, I know about these lousy Disqus ads. Please use adblocker. I would consider to subscribe to 'pro' version of Disqus if the signal/noise ratio in comments would be good enough.