Knuth-Morris-Pratt string-searching algorithm (part II): DFA version

(The following text has been copypasted to the SAT/SMT by example book.)

(See part I.)

I reworked the Java code by Robert Sedgewick from his excellent book, and rewritten it to Python:

#!/usr/bin/env python3

def KMP(pat):
    R=256
    m=len(pat)

    # build DFA from pattern
    # https://stackoverflow.com/questions/2397141/how-to-initialize-a-two-dimensional-array-in-python
    dfa=[[0]*m for r in range(R)]
    dfa[ord(pat[0])][0]=1
    x=0
    for j in range(1, m):
        for c in range(R):
            dfa[c][j] = dfa[c][x]      # Copy mismatch cases. 
        dfa[ord(pat[j])][j] = j+1      # Set match case. 
        x = dfa[ord(pat[j])][x]        # Update restart state. 

    return dfa

# https://stackoverflow.com/questions/3525953/check-if-all-values-of-iterable-are-zero
def all_elements_in_list_are_zeros (l):
    return all(v==0 for v in l)

def export_dfa_to_graphviz(dfa, fname):
    m=len(dfa[0]) # len of pattern
    f=open(fname,"w")
    f.write("digraph finite_state_machine {\n")
    f.write("rankdir=LR;\n")
    f.write("\n")
    f.write("size=\"8,5\"\n")
    f.write(f"node [shape = doublecircle]; S_0 S_{m};\n")
    f.write("node [shape = circle];\n")

    for state in range(m):
        exits=[]
        for R in range(256):
            next=dfa[R][state]
            if next!=0:
                exits.append((R,next))
        for exit in exits:
            next_state=exit[1]
            label="'"+chr(exit[0])+"'"
            s=f"S_{state} -> S_{next_state} [ label = \"{label}\" ];\n"
            f.write (s)
        s=f"S_{state} -> S_0 [ label = \"other\" ];\n"
        f.write (s)
    f.write("}\n")
    f.close()
    print (f"{fname} written")

def search(dfa, txt):
    # simulate operation of DFA on text
    m=len(dfa[0]) # len of pattern
    n=len(txt)
    j=0 # FA state
    i=0
    while i<n and j<m:
        j = dfa[ord(txt[i])][j]
        i=i+1
    if j == m:
        return i - m # found
    return n         # not found

I added a code to produce a graph in GraphViz format.

Now what about the 'ok' word?

Another word we already know, 'eel':

The 'cocos':

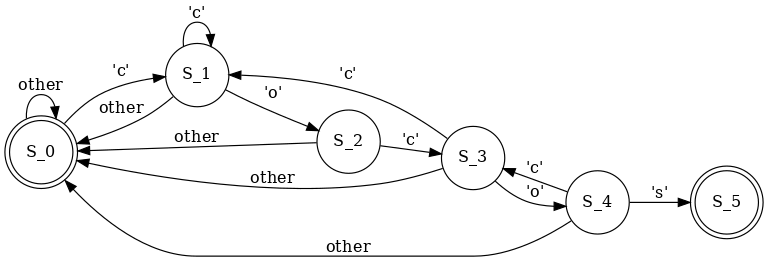
You see, I can translate these FAs (finite automatas) to Python code:

#!/usr/bin/env python3

def search_eel(txt):
    # simulate operation of DFA on text
    m=3 # len of pattern
    n=len(txt)
    j=0 # FA state
    i=0 # iterator for txt[]
    while i<n and j<m:
        ch=txt[i]
        if j==0 and ch=='e':
            j=1
        elif j==1 and ch=='e':
            j=2
        elif j==2 and ch=='e':
            j=2
        elif j==2 and ch=='l':
            j=3
        else:
            j=0 # reset
        i=i+1
    if j == m:
        return i - m # found
    return n         # not found

Do you see any similarities with the C code from the previous part?

The KMP algorithm creates a DFA for each substring to be searched. This is preprocessing.

The DFA is then executes on the input string, in the very same fashion like regular expression matcher.

All the files I used

Part III.

List of my other blog posts.

Yes, I know about these lousy Disqus ads. Please use adblocker. I would consider to subscribe to 'pro' version of Disqus if the signal/noise ratio in comments would be good enough.