
(The following text has been copypasted to the SAT/SMT by example book.)
(See part I.)
I reworked the Java code by Robert Sedgewick from his excellent book, and rewritten it to Python:
#!/usr/bin/env python3
def KMP(pat):
R=256
m=len(pat)
# build DFA from pattern
# https://stackoverflow.com/questions/2397141/how-to-initialize-a-two-dimensional-array-in-python
dfa=[[0]*m for r in range(R)]
dfa[ord(pat[0])][0]=1
x=0
for j in range(1, m):
for c in range(R):
dfa[c][j] = dfa[c][x] # Copy mismatch cases.
dfa[ord(pat[j])][j] = j+1 # Set match case.
x = dfa[ord(pat[j])][x] # Update restart state.
return dfa
# https://stackoverflow.com/questions/3525953/check-if-all-values-of-iterable-are-zero
def all_elements_in_list_are_zeros (l):
return all(v==0 for v in l)
def export_dfa_to_graphviz(dfa, fname):
m=len(dfa[0]) # len of pattern
f=open(fname,"w")
f.write("digraph finite_state_machine {\n")
f.write("rankdir=LR;\n")
f.write("\n")
f.write("size=\"8,5\"\n")
f.write(f"node [shape = doublecircle]; S_0 S_{m};\n")
f.write("node [shape = circle];\n")
for state in range(m):
exits=[]
for R in range(256):
next=dfa[R][state]
if next!=0:
exits.append((R,next))
for exit in exits:
next_state=exit[1]
label="'"+chr(exit[0])+"'"
s=f"S_{state} -> S_{next_state} [ label = \"{label}\" ];\n"
f.write (s)
s=f"S_{state} -> S_0 [ label = \"other\" ];\n"
f.write (s)
f.write("}\n")
f.close()
print (f"{fname} written")
def search(dfa, txt):
# simulate operation of DFA on text
m=len(dfa[0]) # len of pattern
n=len(txt)
j=0 # FA state
i=0
while i<n and j<m:
j = dfa[ord(txt[i])][j]
i=i+1
if j == m:
return i - m # found
return n # not found
I added a code to produce a graph in GraphViz format.
Now what about the 'ok' word?

Another word we already know, 'eel':

The 'cocos':
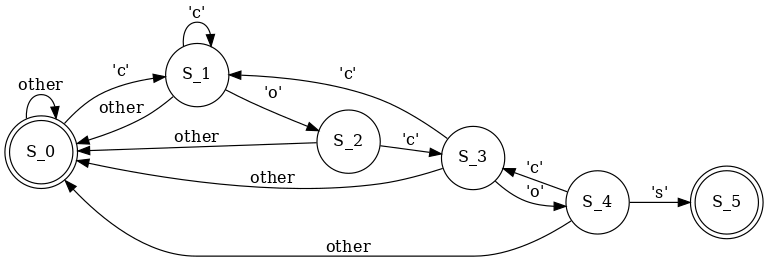
You see, I can translate these FAs (finite automatas) to Python code:
#!/usr/bin/env python3
def search_eel(txt):
# simulate operation of DFA on text
m=3 # len of pattern
n=len(txt)
j=0 # FA state
i=0 # iterator for txt[]
while i<n and j<m:
ch=txt[i]
if j==0 and ch=='e':
j=1
elif j==1 and ch=='e':
j=2
elif j==2 and ch=='e':
j=2
elif j==2 and ch=='l':
j=3
else:
j=0 # reset
i=i+1
if j == m:
return i - m # found
return n # not found
Do you see any similarities with the C code from the previous part?
Yes, what we actually did, was FA, and the 'seen' variable was used as a marker of current state. Here we use the 'j' variable instead, but it's almost the same! We reinvented DFA.The KMP algorithm creates a DFA for each substring to be searched. This is preprocessing.
The DFA is then executes on the input string, in the very same fashion like regular expression matcher.

Yes, I know about these lousy Disqus ads. Please use adblocker. I would consider to subscribe to 'pro' version of Disqus if the signal/noise ratio in comments would be good enough.