
(The following text has been copypasted to the SAT/SMT by example book.)
Some years ago, when i struggled to understand regular expressions, I found these experiments useful. The following is like my student's notes. I hope, someone will find it useful too.
TL;DR: Regular expressions usually used for finding patterns in a string/text and also simple parsing tasks.
This is classic example in many RE tutorials -- a RE that matches both U.S. "color" and British "colour".
I'm going to use libfsm, a tool that can produce a DFA for a specific RE.
This is a DFA for it:

But we are programmers, not mathematicians. libfsm can also produce a pure C function that will behave as this DFA:
int
fsm_main(const char *s)
{
const char *p;
enum {
S0, S1, S2, S3, S4, S5, S6
} state;
state = S0;
for (p = s; *p != '\0'; p++) {
switch (state) {
case S0: /* start */
switch ((unsigned char) *p) {
case 'c': state = S1; break;
default: return -1; /* leaf */
}
break;
case S1: /* e.g. "c" */
switch ((unsigned char) *p) {
case 'o': state = S2; break;
default: return -1; /* leaf */
}
break;
case S2: /* e.g. "co" */
switch ((unsigned char) *p) {
case 'l': state = S3; break;
default: return -1; /* leaf */
}
break;
case S3: /* e.g. "col" */
switch ((unsigned char) *p) {
case 'o': state = S4; break;
default: return -1; /* leaf */
}
break;
case S4: /* e.g. "colo" */
switch ((unsigned char) *p) {
case 'u': state = S5; break;
case 'r': state = S6; break;
default: return -1; /* leaf */
}
break;
case S5: /* e.g. "colou" */
switch ((unsigned char) *p) {
case 'r': state = S6; break;
default: return -1; /* leaf */
}
break;
case S6: /* e.g. "color" */
return -1; /* leaf */
default:
; /* unreached */
}
}
/* end states */
switch (state) {
case S6: return 0x1; /* "colou?r" */
default: return -1; /* unexpected EOT */
}
}
Now this is important part -- this function can be used in place of RE matcher. It will work exactly as it. In fact, it emulates DFA for this RE.
It can be used instead of RE matcher in practice, because it works way faster than any RE library. Of course, it has an obvious limitation -- it's hardcoded/hardwired to a single RE.
It's very easy to implement DFA in hardware:
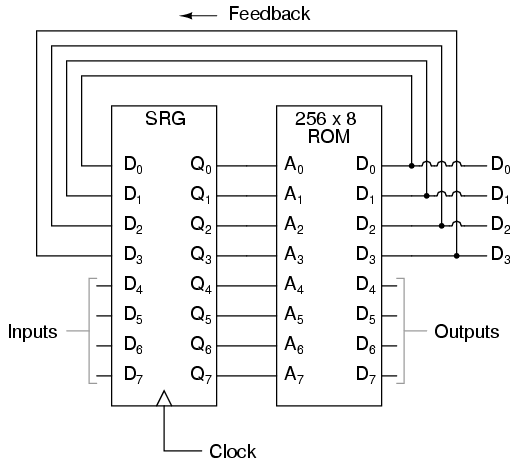
You see, there is only ROM (as a transition function) and (shift) register. Nothing else. (Please ignore 'outputs' at ROM.) This can be implemented in FPGA or ASIC without any problem. In practice, it can filter a voluminous network traffic for a pattern or RAM: without using a CPU or GPU. So if your FPGA/ASIC is clocked at 1GHz, it can process $10^9$ symbols per second, no matter how complex your RE is.
... to be matched with main BSD forks.

int
fsm_main(const char *s)
{
const char *p;
enum {
S0, S1, S2, S3, S4, S5, S6, S7, S8, S9,
S10, S11, S12
} state;
state = S0;
for (p = s; *p != '\0'; p++) {
switch (state) {
case S0: /* start */
switch ((unsigned char) *p) {
case 'N': state = S1; break;
case 'O': state = S2; break;
case 'F': state = S3; break;
default: return -1; /* leaf */
}
break;
case S1: /* e.g. "N" */
switch ((unsigned char) *p) {
case 'e': state = S12; break;
default: return -1; /* leaf */
}
break;
case S2: /* e.g. "O" */
switch ((unsigned char) *p) {
case 'p': state = S10; break;
default: return -1; /* leaf */
}
break;
case S3: /* e.g. "F" */
switch ((unsigned char) *p) {
case 'r': state = S4; break;
default: return -1; /* leaf */
}
break;
case S4: /* e.g. "Fr" */
switch ((unsigned char) *p) {
case 'e': state = S5; break;
default: return -1; /* leaf */
}
break;
case S5: /* e.g. "Fre" */
switch ((unsigned char) *p) {
case 'e': state = S6; break;
default: return -1; /* leaf */
}
break;
case S6: /* e.g. "Net" */
switch ((unsigned char) *p) {
case 'B': state = S7; break;
default: return -1; /* leaf */
}
break;
case S7: /* e.g. "NetB" */
switch ((unsigned char) *p) {
case 'S': state = S8; break;
default: return -1; /* leaf */
}
break;
case S8: /* e.g. "NetBS" */
switch ((unsigned char) *p) {
case 'D': state = S9; break;
default: return -1; /* leaf */
}
break;
case S9: /* e.g. "NetBSD" */
return -1; /* leaf */
case S10: /* e.g. "Op" */
switch ((unsigned char) *p) {
case 'e': state = S11; break;
default: return -1; /* leaf */
}
break;
case S11: /* e.g. "Ope" */
switch ((unsigned char) *p) {
case 'n': state = S6; break;
default: return -1; /* leaf */
}
break;
case S12: /* e.g. "Ne" */
switch ((unsigned char) *p) {
case 't': state = S6; break;
default: return -1; /* leaf */
}
break;
default:
; /* unreached */
}
}
/* end states */
switch (state) {
case S9: return 0x1; /* "(Net|Open|Free)BSD" */
default: return -1; /* unexpected EOT */
}
}
... to be matched with steven/stephen/steve/stevie, but also the first letter can be captial.
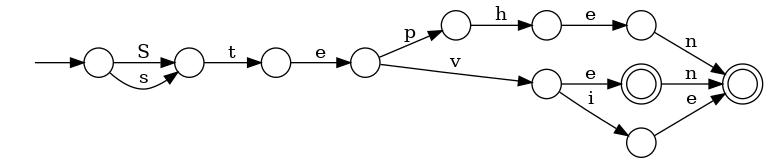
This is important: there are two accepting states (in double circles). How it can be handled in C? (States S6 and S8.)
int
fsm_main(const char *s)
{
const char *p;
enum {
S0, S1, S2, S3, S4, S5, S6, S7, S8, S9,
S10
} state;
state = S0;
for (p = s; *p != '\0'; p++) {
switch (state) {
case S0: /* start */
switch ((unsigned char) *p) {
case 'S':
case 's': state = S1; break;
default: return -1; /* leaf */
}
break;
case S1: /* e.g. "s" */
switch ((unsigned char) *p) {
case 't': state = S2; break;
default: return -1; /* leaf */
}
break;
case S2: /* e.g. "st" */
switch ((unsigned char) *p) {
case 'e': state = S3; break;
default: return -1; /* leaf */
}
break;
case S3: /* e.g. "ste" */
switch ((unsigned char) *p) {
case 'p': state = S4; break;
case 'v': state = S5; break;
default: return -1; /* leaf */
}
break;
case S4: /* e.g. "step" */
switch ((unsigned char) *p) {
case 'h': state = S9; break;
default: return -1; /* leaf */
}
break;
case S5: /* e.g. "stev" */
switch ((unsigned char) *p) {
case 'e': state = S6; break;
case 'i': state = S7; break;
default: return -1; /* leaf */
}
break;
case S6: /* e.g. "steve" */
switch ((unsigned char) *p) {
case 'n': state = S8; break;
default: return -1; /* leaf */
}
break;
case S7: /* e.g. "stevi" */
switch ((unsigned char) *p) {
case 'e': state = S8; break;
default: return -1; /* leaf */
}
break;
case S8: /* e.g. "stevie" */
return -1; /* leaf */
case S9: /* e.g. "steph" */
switch ((unsigned char) *p) {
case 'e': state = S10; break;
default: return -1; /* leaf */
}
break;
case S10: /* e.g. "stephe" */
switch ((unsigned char) *p) {
case 'n': state = S8; break;
default: return -1; /* leaf */
}
break;
default:
; /* unreached */
}
}
/* end states */
switch (state) {
case S6: return 0x1; /* "(s|S)t(even|ephen|eve|evie)" */
case S8: return 0x1; /* "(s|S)t(even|ephen|eve|evie)" */
default: return -1; /* unexpected EOT */
}
}
... something more advanced. Here we see a limitation of DFA. (Well, not a limitation.) This DFA is correct. But it will be more (visually) easier to represent it in NFA, but this is another story.
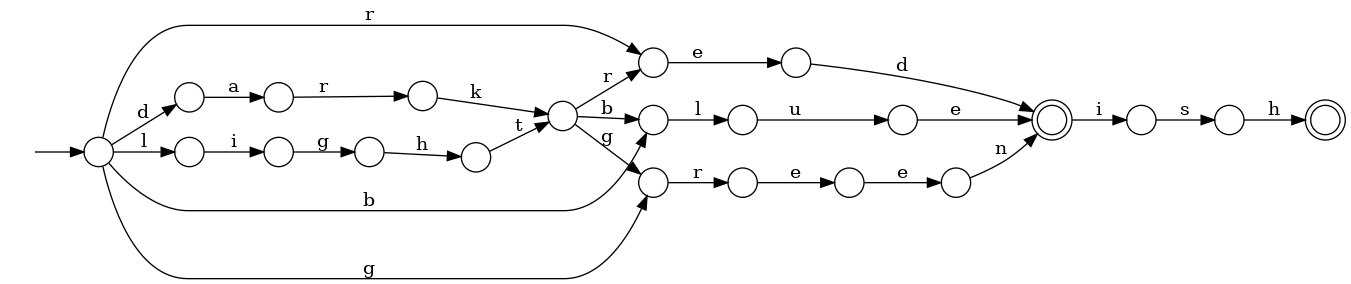
BTW, libfsm can produce a JSON file with all transitions between all the vertices:
{
"statecount": 22,
"start": 9,
"end": [ 5, 11 ],
"edges": [
{ "src": 0, "dst": 2, "symbol": "e" },
{ "src": 1, "dst": 17, "symbol": "u" },
{ "src": 2, "dst": 11, "symbol": "d" },
{ "src": 3, "dst": 4, "symbol": "g" },
{ "src": 4, "dst": 16, "symbol": "h" },
{ "src": 6, "dst": 1, "symbol": "l" },
{ "src": 7, "dst": 6, "symbol": "b" },
{ "src": 7, "dst": 15, "symbol": "g" },
{ "src": 7, "dst": 0, "symbol": "r" },
{ "src": 8, "dst": 3, "symbol": "i" },
{ "src": 9, "dst": 6, "symbol": "b" },
{ "src": 9, "dst": 13, "symbol": "d" },
{ "src": 9, "dst": 15, "symbol": "g" },
{ "src": 9, "dst": 8, "symbol": "l" },
{ "src": 9, "dst": 0, "symbol": "r" },
{ "src": 10, "dst": 21, "symbol": "e" },
{ "src": 11, "dst": 20, "symbol": "i" },
{ "src": 12, "dst": 14, "symbol": "r" },
{ "src": 13, "dst": 12, "symbol": "a" },
{ "src": 14, "dst": 7, "symbol": "k" },
{ "src": 15, "dst": 10, "symbol": "r" },
{ "src": 16, "dst": 7, "symbol": "t" },
{ "src": 17, "dst": 11, "symbol": "e" },
{ "src": 18, "dst": 5, "symbol": "h" },
{ "src": 19, "dst": 11, "symbol": "n" },
{ "src": 20, "dst": 18, "symbol": "s" },
{ "src": 21, "dst": 19, "symbol": "e" }
]
}
And I wrote a simple utility to enumerate all possible input strings that this DFA will accept, in Racket. It is trivial. It just traverses a DFA recursively down to all accepting states.
#lang racket
(require json)
(define cmd (current-command-line-arguments))
(when (= (vector-length cmd) 0)
(displayln "usage: fname.json")
(exit))
(define fname (vector-ref cmd 0))
; knobs:
(define traverse-strlen-limit 15)
(define strings-limit 500000)
(define a (read-json (open-input-file fname)))
;a
(define accepted-states (hash-ref a 'end))
(define start-state (hash-ref a 'start))
(define statecount (hash-ref a 'statecount))
(define tbl (make-hash))
(for ([x (hash-ref a 'edges)])
(let [(src (hash-ref x 'src))
(dst (hash-ref x 'dst))
(symbol (hash-ref x 'symbol))]
(hash-update! tbl src
(lambda (x) (cons (list dst symbol) x))
'())))
;tbl
(define count 0) ; ah! a global variable
(define (traverse-DAG-recursively tbl start cur-string)
(when (< (string-length cur-string) traverse-strlen-limit)
(when (member start accepted-states)
(displayln (string-append "string matched: [" cur-string "]"))
(set! count (add1 count))
(when (> count strings-limit)
(displayln "strings-limit reached, exiting")
(exit)))
(when (hash-has-key? tbl start)
(for/list ([i (hash-ref tbl start)])
(traverse-DAG-recursively tbl (first i) (string-append cur-string (second i)))))))
(void (traverse-DAG-recursively tbl start-state ""))
(displayln (string-append "total: " (number->string count)))
What it will say for that DFA?
string matched: [red] string matched: [redish] string matched: [lightred] string matched: [lightredish] string matched: [lightgreen] string matched: [lightgreenish] string matched: [lightblue] string matched: [lightblueish] string matched: [green] string matched: [greenish] string matched: [darkred] string matched: [darkredish] string matched: [darkgreen] string matched: [darkgreenish] string matched: [darkblue] string matched: [darkblueish] string matched: [blue] string matched: [blueish] total: 18
UPD: discussion at HN and reddit.

Yes, I know about these lousy Disqus ads. Please use adblocker. I would consider to subscribe to 'pro' version of Disqus if the signal/noise ratio in comments would be good enough.