
From school trigonometry, we may remember that angles are measured in degrees. (360° is a full circle.)
But in mathematics, radians are way more popular. $2\pi$ is a full circle, etc.
sin()/cos() library functions of many programming languages use radians.
The following JS code draws 12 clock hands. String for each hand -- is a value in radians. Full circle in clock are 12 hours. So we should divide full circle by 12.
Hence, the angle between two consecutive hours is $\frac{2\pi}{12}$.
<!doctype html>
<html>
<head>
<style>
#my-canvas { border: 1px solid gray; }
</style>
</head>
<body>
<canvas id="my-canvas" width="600" height="600"></canvas>
<script>
var canvas = document.querySelector('#my-canvas');
var context = canvas.getContext('2d');
var half_width = canvas.width/2;
var half_height = canvas.height/2;
// clock is slightly smaller than canvas:
var clock_radius = Math.min(half_width, half_height)*0.85;
function drawLine(x1, y1, x2, y2)
{
context.beginPath();
context.moveTo(x1+half_width, y1+half_height);
context.lineTo(x2+half_width, y2+half_height);
context.stroke();
};
function putText(x, y, text)
{
context.font = "18px Arial";
context.fillText(text, x+half_width, y+half_height);
};
function clock()
{
for (angle=0; angle<=2*Math.PI; angle=angle+((2*Math.PI)/12))
{
var x=Math.sin(angle)*clock_radius;
var y=-Math.cos(angle)*clock_radius;
drawLine(0, 0, x, y);
putText(x, y, angle.toFixed(2).toString());
};
};
clock();
</script>
</body>
</html>
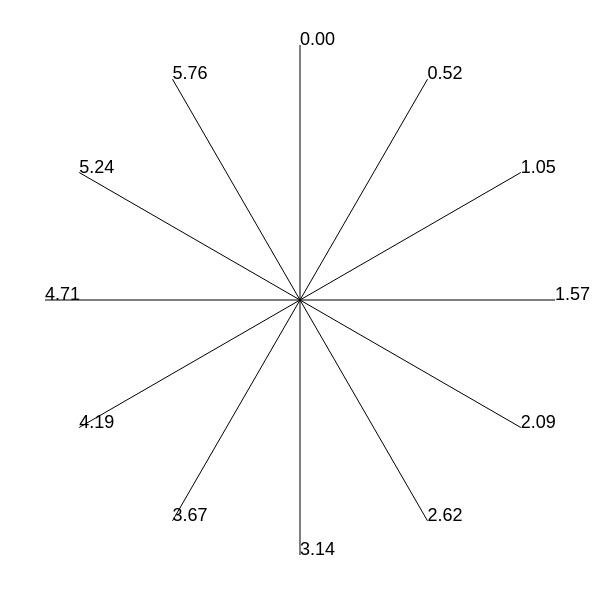
A little more tinkering, and you will be able to draw a hour hand for the current time.
From wikipedia, you may know that sin() and cos() are basically the same function. But one is shifted by $\frac{\pi}{2}$ or by 90°.
Hence, we can rework this example to use only sin() or only cos():
for (angle=0; angle<=2*Math.PI; angle=angle+((2*Math.PI)/12))
{
var x=-Math.cos(angle+Math.PI/2)*clock_radius;
var y=-Math.cos(angle)*clock_radius;
drawLine(0, 0, x, y);
putText(x, y, angle.toFixed(2).toString());
};
for (angle=0; angle<=2*Math.PI; angle=angle+((2*Math.PI)/12))
{
var x=Math.sin(angle)*clock_radius;
var y=-Math.sin(angle+Math.PI/2)*clock_radius;
drawLine(0, 0, x, y);
putText(x, y, angle.toFixed(2).toString());
};
The 90° arc ($\frac{1}{4}$) is symmetrical, so it's possible.
You also need a minute hand for clock. It can be drawed in the same manner, but divide circle by 60:
function clock()
{
for (angle=0; angle<=2*Math.PI; angle=angle+((2*Math.PI)/60))
{
var x=Math.sin(angle)*clock_radius;
var y=-Math.cos(angle)*clock_radius;
drawLine(0, 0, x, y);
putText(x, y, angle.toFixed(2).toString());
};
};
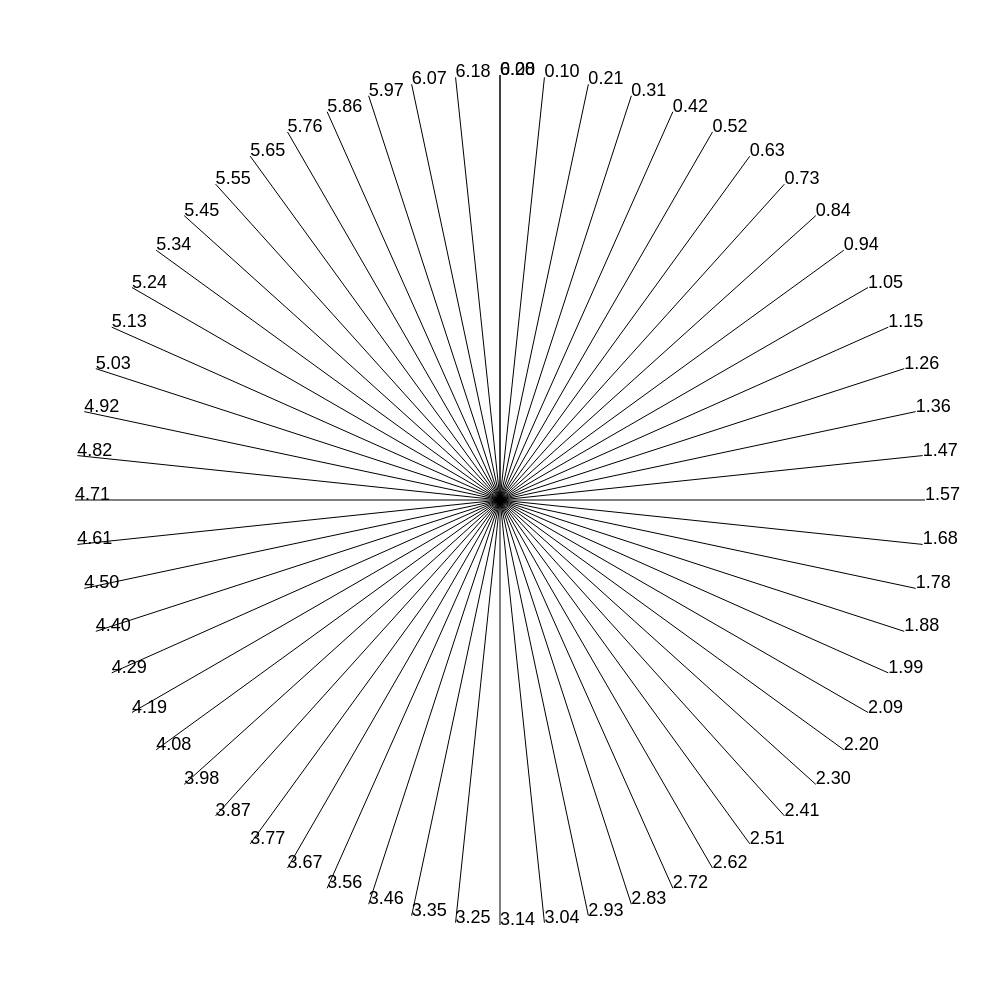
Precomputed tables were quite common in demomaking, demos/intros that could run on old 80386 CPU without FPU coprocessor. And even if FPU coprocessor is present, it's always slower than table lookup.
Today, this is the case of cheap microcontrollers with no FPU, that would draw a clock on a LED display maybe. High precision isn't important -- all you want is to find right pixel or LED, to fire it.
Such a table can contain only 60 elements with x/y coordinates for each. And since a clock/circle is symmetrical (at least four parts are symmetrical copies, rotated), only 60/4=15 elements are enough.
This is the case of Windows OS clock. (It is true at least for Windows 7, maybe newer versions have this too as well.) Somehow, they still have table-based sin()/cos() for drawing hands -- but 30 elements in table. (More information about it is in my book.)
I could stand the urge and tried 256 hands, 512, 1024. Nice graphics effects surfaced:
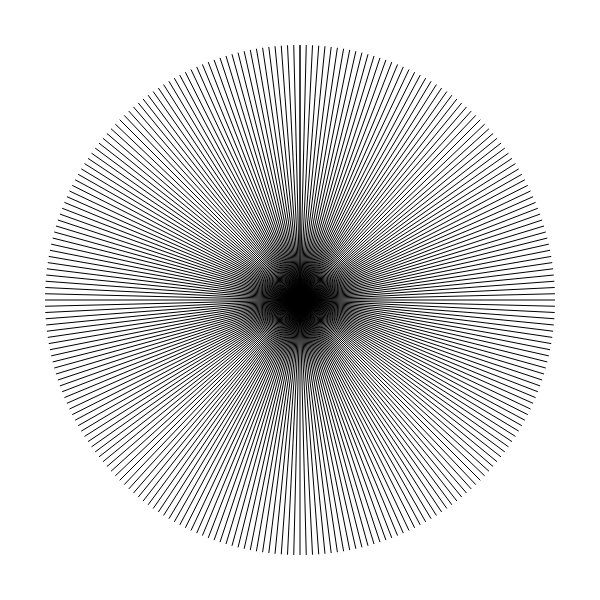
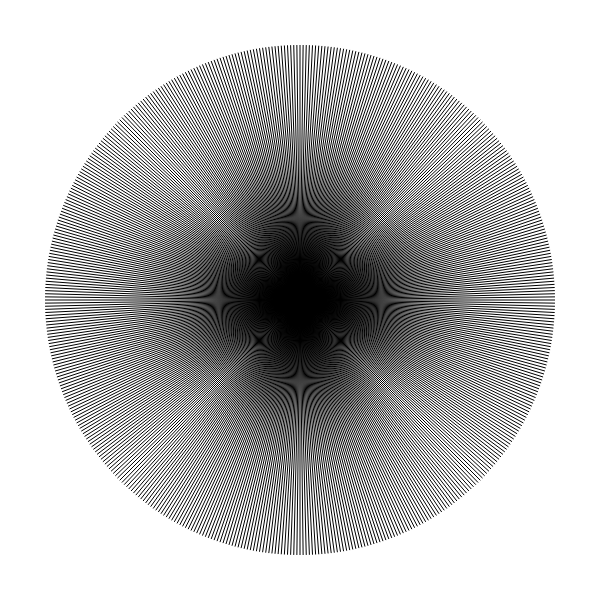

As a home work, you can try to explain these effects/artefacts.
(UPD: 20240517 01:02:28 EEST. Bug fixed by DarkLord.)
Yes, I know about these lousy Disqus ads. Please use adblocker. I would consider to subscribe to 'pro' version of Disqus if the signal/noise ratio in comments would be good enough.