[Math] Calculus: derivatives of x^2 and x^3: visual demonstration

My previous blog posts about calculus and derivatives: 1, 2.

See also chapter 5 here.

And so, this code generates two similar tables, but the second part is slightly faster:

#!/usr/bin/env python3

for x in range(15):
    print (x, x*x)

print ("")

a=0
for x in range(15):
    print (x, a)
    a = a + 2*x + 1

Let's see why increasing square by 2x+1 is like recalculating square at each iteration.

Imagine a square with 4 'dots' side:

****
****
****
****

How would you grow it by 1 'dot'? Add a line at top and at right:

++++.
****+
****+
****+
****+

There are two lines of length 4 '+' and also one corner '.'. The resulting square has side of 5 dots.

So, in the 2x+1 expression, 2x is the number of '+' to by added in two 'lines', and +1 is that corner '.'.

This how you 'grow' square without recalculating x^2. And that may be faster sometimes, as I stated before.

Now about x^3:

#!/usr/bin/env python3

for x in range(0, 15):
    print (x, x*x*x)

print ("")

a=0
for x in range(0, 15):
    print (x, a)
    a = a + 3*x*x + x*3 + 1

To grow a cube, you add this number of 'dots': 3x^2 + 3x + 1.

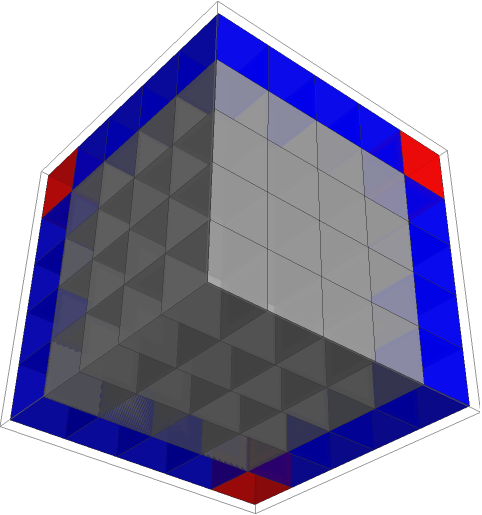
I'm going to demonstrate all this visually. Here is a cube with side of 4 cubelets. 4*4*4 cube is gray:

How do you 'grow' it?

You add 3 square plates of size 4*4 to 3 sides of cube: blue cubelets: 3x^2 of them.
There are also 3 red 'lines' to cover newly formed 'trenches': 3x of them.
And there is also one single green 'corner' cubelet to be added: +1.

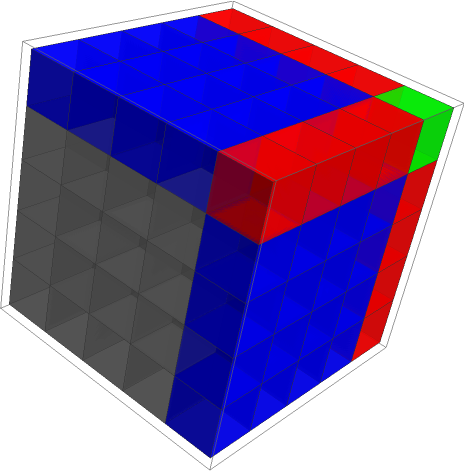
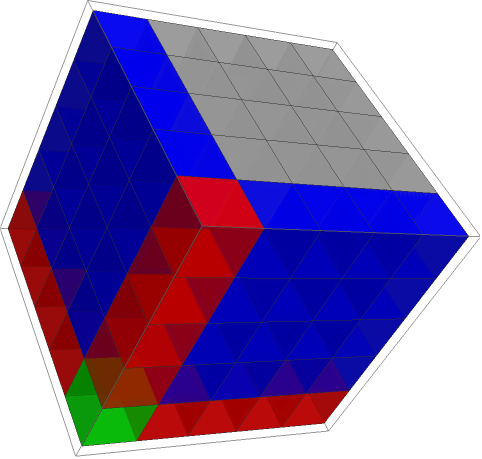
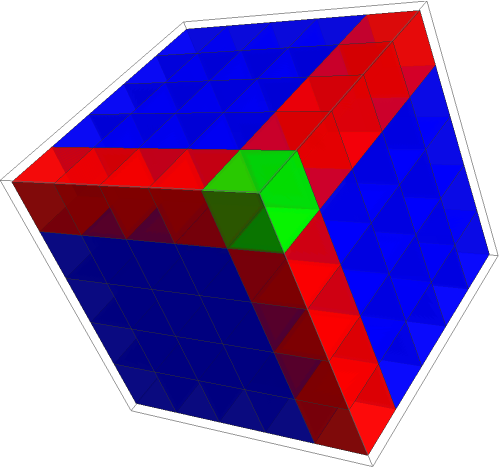
Thus you can 'grow' a cube without recalculating x^3 each time, with the help of calculus. These expressions are actually derivatives of x^2 and x^3.

Also, Wolfram Mathematica notebook I used is here.

Further work -- tesseract.

(the post first published at 20240710.)

List of my other blog posts.

Subscribe to my news feed,

Yes, I know about these lousy Disqus ads. Please use adblocker. I would consider to subscribe to 'pro' version of Disqus if the signal/noise ratio in comments would be good enough.