[Math] Walking passwords

I've seen walking password only once in my life, something like '3edfr45tgh' -- the password for ISP in 1990s. The bonus of walking password is that it's easy to memorize -- that walking pattern on keyboard. By the way, that reminds us guitar tablatures.

Also, the password used once by Brian Kernighan was '/.,/.,,' -- almost like walking password.

Walking passwords in SecLists:

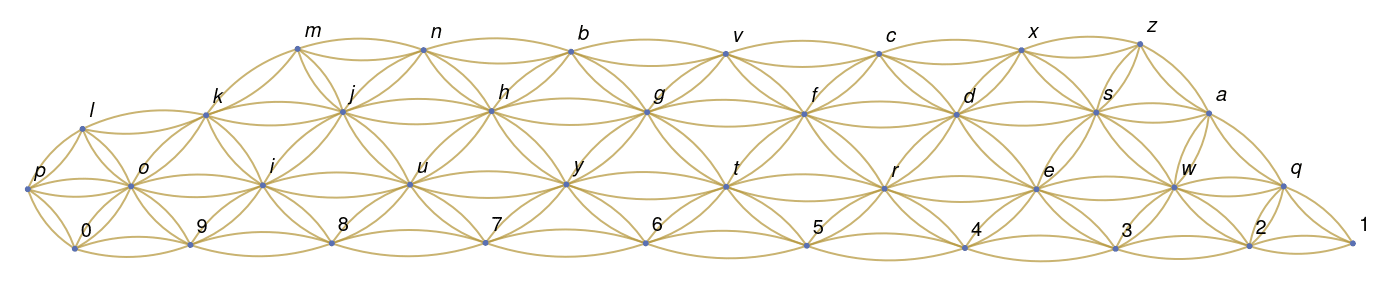
Keyboard walks, also sometimes known as waterfalls or "spatial pattern" passwords, are passwords generated by typing adjacent keys on the keyboard, with [SHIFT] held occasionally in order to meet common complexity requirements (i.e. capital letters + symbols). These passwords may resemble randomly generated strings but are not nearly as strong, as they often follow predictable patterns and are easy to guess despite meeting length and complexity requirements. Due to both the structure of the QWERTY keyboard and human preferences for memory chunking, most keyboard walks tend to consist of multiples of four characters (4, 8, 12, 16, etc.)

Wolfram Mathematica:

In[2]:= gg=Graph[{1<->2,1<->q,2<->1,2<->3,2<->q,2<->w,3<->2,3<->4,3<->w,3<->e,4<->3,4<->5,4<->e,4<->r,
5<->4,5<->6,5<->r,5<->t,6<->5,6<->7,6<->t,6<->y,7<->6,7<->8,7<->y,7<->u,8<->7,8<->9,8<->u,8<->i,9<->8,
9<->0,9<->i,9<->o,0<->9,0<->o,0<->p,q<->w,q<->1,q<->2,q<->a,w<->q,w<->e,w<->2,w<->3,w<->a,w<->s,e<->w,
e<->r,e<->3,e<->4,e<->s,e<->d,r<->e,r<->t,r<->4,r<->5,r<->d,r<->f,t<->r,t<->y,t<->5,t<->6,t<->f,t<->g,
y<->t,y<->u,y<->6,y<->7,y<->g,y<->h,u<->y,u<->i,u<->7,u<->8,u<->h,u<->j,i<->u,i<->o,i<->8,i<->9,i<->j,
i<->k,o<->i,o<->p,o<->9,o<->0,o<->k,o<->l,p<->o,p<->0,p<->l,a<->s,a<->q,a<->w,a<->z,s<->a,s<->d,s<->w,
s<->e,s<->z,s<->x,d<->s,d<->f,d<->e,d<->r,d<->x,d<->c,f<->d,f<->g,f<->r,f<->t,f<->c,f<->v,g<->f,g<->h,
g<->t,g<->y,g<->v,g<->b,h<->g,h<->j,h<->y,h<->u,h<->b,h<->n,j<->h,j<->k,j<->u,j<->i,j<->n,j<->m,k<->j,
k<->l,k<->i,k<->o,k<->m,l<->k,l<->o,l<->p,z<->x,z<->a,z<->s,x<->z,x<->c,x<->s,x<->d,c<->x,c<->v,c<->d,
c<->f,v<->c,v<->b,v<->f,v<->g,b<->v,b<->n,b<->g,b<->h,n<->b,n<->m,n<->h,n<->j,m<->n,m<->j,m<->k},
VertexLabels->"Name"]

In[4]:= vertices=VertexList[gg];
In[5]:= pairs=Tuples[{vertices,vertices}]; (*cartesian product*)
In[6]:= paths=Flatten[DeleteCases[Map[FindPath[gg,#[[1]],#[[2]],{8(*path length in edges*)},
10^8(*generate as much as possible paths*)]&,pairs],{}],1]

Out[6]= {{1,q,a,z,x,d,s,w,2},{1,q,a,z,x,d,e,w,2},{1,q,a,z,x,d,e,3,2},{1,q,a,z,x,s,e,w,2},
{1,q,a,z,x,s,e,3,2}, ... ,{m,j,u,7,6,y,g,b,n},{m,j,u,7,6,y,g,h,n},{m,j,u,7,6,t,g,b,n},
{m,j,u,7,6,t,g,h,n},{m,j,u,7,6,t,y,h,n}}

In[7]:= passwords=Map[StringTrim[StringDelete[ToString[#],", "],("{"|"}")]&,paths];

In[8]:= Length@passwords
Out[8]= 673986

In[9]:= passwords[[1;;20]](*sample*)
Out[9]= {1qazxdsw2,1qazxdew2,1qazxde32,1qazxsew2,1qazxse32,1qazxsw32,1qazsdew2,1qazsde32,1qazse432,
1qazsew32,1qazse3w2,1qazswe32,1qasxdew2,1qasxde32,1qasdrew2,1qasdre32,1qasdr432,1qasde432,1qasdew32,
1qasde3w2}

In[11]:= Export["~/tmp/walk_pw_8.txt",passwords];

In[13]:= RandomSample[passwords,20]
Out[13]= {wedrtyhju,ew2qasxdc,aq23edsxc,fghyuiop0,tfgyu78io,gt67yuhbv,89okmjhbv,6tgyhnbvc,mnbgy7ujh,
5r43edxsa,23wsxcdre,o9876ytfr,cfvbghy78,6y7u8ikjn,wasdertyh,xsdrtgy67,ijhyt5r43,3w2qazxcv,cdr5tyhgb,
jhnbvft54}

Graph rendered by Wolfram Mathematica is similar visually to a keyboard, but mirrored horizontally/vertically (or rotated):

Of course, such passwords are so weak, because there are so small list of them. And of course, passwords in other languages are no stronger. Further work: handle shifts, capital letters, special characters.

If you dislike Wolfram Mathematica, you can use the Python networkx library or google for the 'graph library' for your favorite PL. There are many.

All the files I used, including Mathematica notebook.

(the post first published at 20240813.)

List of my other blog posts.

Subscribe to my news feed,

Yes, I know about these lousy Disqus ads. Please use adblocker. I would consider to subscribe to 'pro' version of Disqus if the signal/noise ratio in comments would be good enough.